En | Fr

Operations World

Tap graphic from the home page to visit the Operations World.

Basics

  • Tap one finger on the screen to create a 1.
  • Tap a number of fingers (more than one) at once on the screen to create that number. (To create a number larger than 10, keep tapping some fingers without ever letting go of all of them at once.)
  • Drag a number to move it.
  • Push two or more numbers together with two or more fingers to add them into a new number, their sum.
  • Pull a number apart with multiple fingers to split it into smaller parts.
    • The first finger holds the original number still, while other fingers split away parts of it.
    • The farther you pull, the larger the part you split away from the original whole.
    • Splitting is fair: multiple parts split simultaneously are always equal in size.
  • Tap reset icon Reset to erase all numbers.
  • Tap back icon Back to leave the Operations World and return to the home page.
  • Visit settings icon Settings on the home page to choose the language in which new numbers are named.

Activities

Make a 1 and 4. Push them together to make 5. What are other ways to make 5? How many different ways can you make 5?
Make a 5 and a 3. What happens if you pinch them together? Can you pull them apart into two equal pieces?
Make a 5 and another 5. Pinch them together. What did you get? Make some more of these by different ways. How many do you need in order to make 100 in all?
Teacher makes 1, 2, 3, 4 and 5 placed randomly on the screen and asks: can you place these in order?
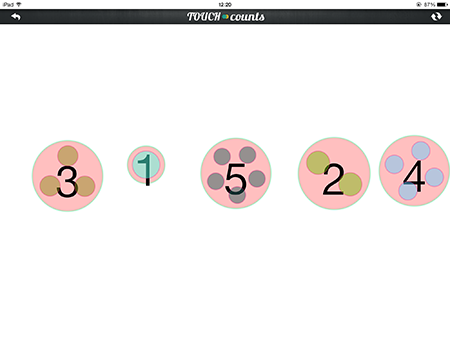Make a bunch of different numbers. Which is biggest? Which is smallest? Can you put them in order?
Make a 5 all by itself. Hold it with one finger and use another to pull out 2. What numbers do you have left on the screen? What would happen if you pinched them together?
Make a 20 all by itself. Try to split it into four equal numbers. What happens if you put them all back together again?
Teacher makes several 1s, 2s, 3s and 4s and challenges children to use these numbers to make 5s (or any other target number)
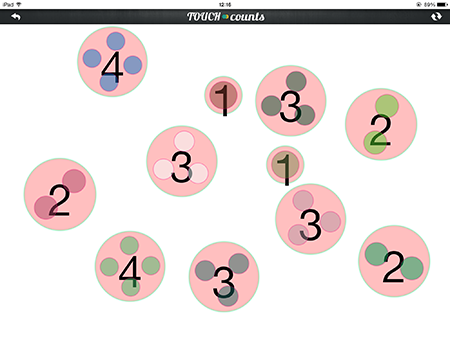Teacher makes a 6 and holds it still with one finger while two children split away equal-sized parts by dragging. Does anything remain? How many parts result, of what values? Now push the parts together back into 6 and try again. How many different arrangements of parts can you make, from 6?
Repeat the last experiment starting with 7. Repeat a third time starting with 12.
Make a 24. How can you split it into the smallest number of equal-sized parts (with no remainder)?
Repeat the last experiment starting with 33.

Teacher Notes

In the Operations World, children can use gestures to develop a sense of the basic operations of adding and partitioning (a precursor to subtracting). When working in this world, children are using the cardinality principle as they operate on numbers either by pinching them together (to add) or pulling them apart (to subtract or partition).

Because TouchCounts computes the sum and the difference, children focus on how these operations work—in terms of their results—and how they complement each other. Colourcoding of pinched-together numbers helps show where these numbers “come from,” by preserving a trace of the addends in the new, composite sum. Number magnitude is subtly reinforced by visible size variations between numbers of very different magnitudes, and symbolic naming by always displaying a number both as a set of identical objects and as a corresponding written numeral.

Finally, splitting quantities into multiple equal-sized parts—equipartioning—is an important foundation for division that is entirely accessible at the pre-school level. Conversely, adding together two or more identical quantities simultaneously can be an important experiential precursor to multiplication.

See the Research Bibliography for additional information.